Confusion Matrix (분류 모델 성능 평가지표)

Confusion Matrix는 분류 모델에서 가장 많이 쓰이고 있는 지표입니다.

 

 

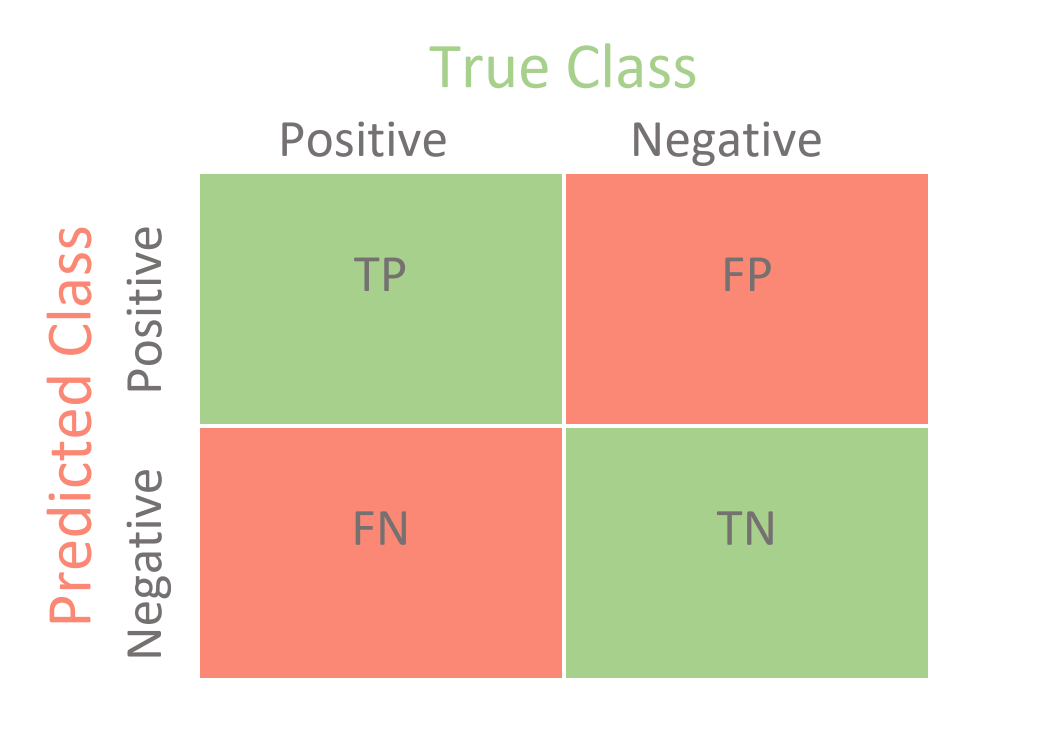
모델이 정답을 맞춘 케이스

TP - 정답이 Positive이고 분류 모델이 Positive으로 예측한 케이스 

TN - 정답이 Negative이고 분류 모델이 Negative으로 예측한 케이스

 

모델이 정답을 못 맞춘 케이스

FP - 정답이 Positive이고 분류 모델이 Negative으로 예측한 케이스

FN - 정답이 Negative이고 분류 모델이 Positive으로 예측한 케이스

 

1. 정확도(Accuracy) 측정

정확도는 실제 정답을 바르게 예측한 비율

 

정확도 = (TP+TN) / (TP+FP+FN+TN)

 

2. 정밀도(Precision) 측정

정밀도는 모델이 Positive으로 예측한 값이 실제 Positive인 비율

 

정밀도 = TP / (TP+FP)

 

3. 재현도(Recall) 측정

재현도는 실제값이 Positive인 값들 중 모델이 Positive으로 예측한 비율

 

재현도 = TP / (TP+FN)

 

4. F-1 Score 측정

정밀도(Precision)와 재현도(Recall)의 조화 평균

 

F1-Score = (2 x precision x recall) / (precision+recall)

 

 

Accuracy 대신 정밀도, 재현도, F-1 Score를 구하는 이유는

1. 불균형한 Positive/Negative 비율을 가지고 있는 데이터셋

실제 우리가 사용하고 있는 데이터셋은 Positive과 Negative 비율이 일정하지 않다.

Positive, Negative 비율을 균등하게 측정하기 위해서는 단순 정확도보다는 다각도로 분석하는 정밀도, 재현도, F1-Score 측정 방법이 필요하다.

 

2. 분류 모델이 Positive 혹은 Negative 한쪽으로 치우쳐서 예측하는지 확인 필요

Positive - 1000건 / Negative - 1000 건으로 가정을 하면,

Positive을 Positive으로 100% 맞게 예측하고 Negative을 50%만 맞게 예측하면 전체적인 정확도는 75%이다.

하지만, Negative인 정답을 반은 Positive, 반은 Negative으로 예측하고 있는 상황이기 때문에,

실제 Negative은 전혀 예측을 잘 못하고 있는 상황이다.

 

이를 방지하기 위해서, 분류 모델은 다각도의 측정 방법론이 필요하다.

 

분류 모델 측정 방법의 중요성 (예시)

실제 예시로, 보험 회사에서 적용된 분류 모델을 말씀드리자면

고객의 프로필을 기반으로 해당 고객이 암이 걸릴지 걸리지 않을지 예측을 해서 틀린 경우를 살펴보면,

 

1. 고객이 암에 걸리지 않지만 고객이 암에 걸린다고 예측할 경우

2. 고객이 암에 걸리지만 고객이 암에 걸리지 않는다고 예측할 경우

 

1번 케이스는 고객이 암에 걸린다고 예측을 하기 때문에 고객으로 유치하지 않을 대상으로 여기기 때문에,

고객이 수납하는 월 보험료 받지 못하는 손해 발생

 

2번 케이스는 고객이 암에 걸리지 않는다고 예측하기 때문에 고객으로 유치를 하지만,

실제 암에 걸려서 치료비를 고객에게 제공해야되는 손해 발생

 

동일하게 틀린 케이스지만, 2번 케이스가 보험사 입장에서는 매우 큰 손해를 발생시키는 상황이다.

결론은 정확도도 중요하지만, 분류 모델 내에서는 정확도가 모델을 평가하는 지표가 되면 좋다고 얘기할수가 없다.